
Windows: DEMO_XY.exe 18 Linux: ./DEMO_XY.run 18
The problem has been outlined in books devoted to electron optics (multiple symmetry lenses), e.g. Szymański, Mulak, Duda, Romanowski, "Electron Optics", 2nd edition, Wydawnictwa Naukowo Techniczne, Warsaw 1984. Szymański's book mentioned the asymmetrical distribution of electrodes.
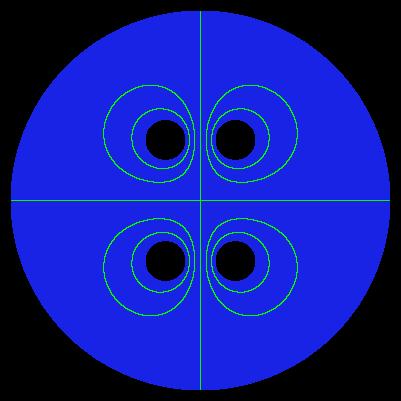
Each pixel represents one mesh point.
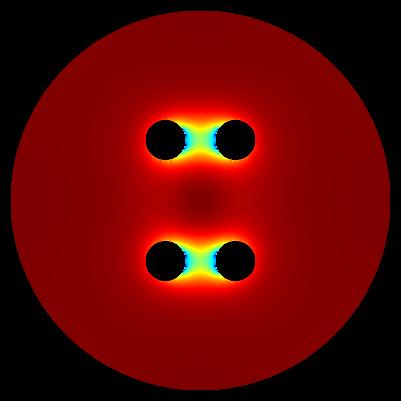
colour white - vacuum colour red - casing 1 (U = +0.0 [V]) colour green - electrodes 2 (U = +1.0 [V]) colour blue - electrodes 3 (U = -1.0 [V])

mesh size: number of rows == 401 number of columns == 401 x == -200.0 ... +200.0 [mm] y == -200.0 ... +200.0 [mm] number of iterations >>> SUCCESS - solution V(x,y) has been found after 25513 iterations pi constant: M_PI == +3.14... electrode type 1 (casing, red) boundary == +1 voltage == +0.0 [V] x_center == +0.0 [mm] y_center == +0.0 [mm] radius >= +190.0 [mm] electrodes type 2 (2 elements, green) boundary == +2 voltage == +1.0 [V] radius <= +20.0 [mm] N == +6 /* hexapole without some elements */ alpha_zero == +0.0 [rad] R == +50.0 [mm] coordinates of centres of electrodes type 2: 1/2 n = +2 x_3 = R * cos(alpha_zero + 2 * n * M_PI / N); y_3 = R * sin(alpha_zero + 2 * n * M_PI / N); 2/2 n = +4 x_5 = R * cos(alpha_zero + 2 * n * M_PI / N); y_5 = R * sin(alpha_zero + 2 * n * M_PI / N); electrodes type 3 (2 elements, blue) boundary == +3 voltage == -1.0 [V] radius <= +20.0 [mm] N == +6 /* hexapole without some elements */ alpha_zero == +0.0 [rad] R == +50.0 [mm] coordinates of centres of electrodes type 3: 1/2 n = +1 x_2 = R * cos(alpha_zero + 2 * n * M_PI / N); y_2 = R * sin(alpha_zero + 2 * n * M_PI / N); 2/2 n = +5 x_6 = R * cos(alpha_zero + 2 * n * M_PI / N); y_6 = R * sin(alpha_zero + 2 * n * M_PI / N); computation accuracy: eps == 1.0E-9 [V]


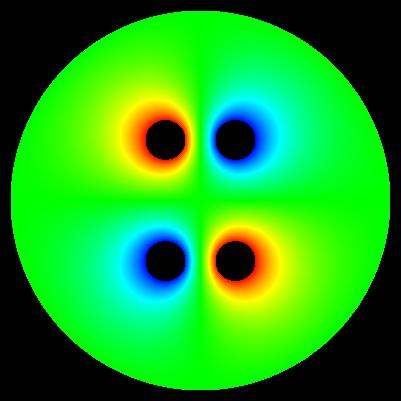
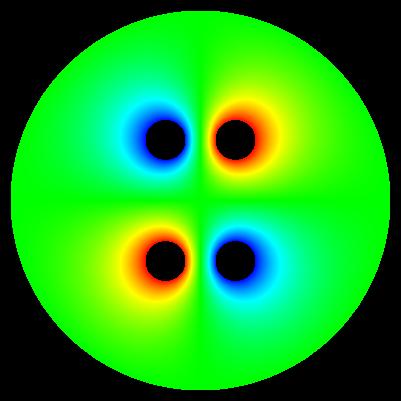
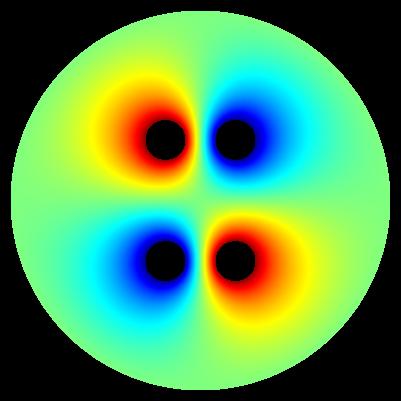
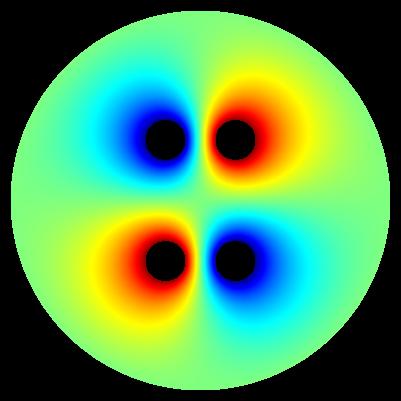
Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.


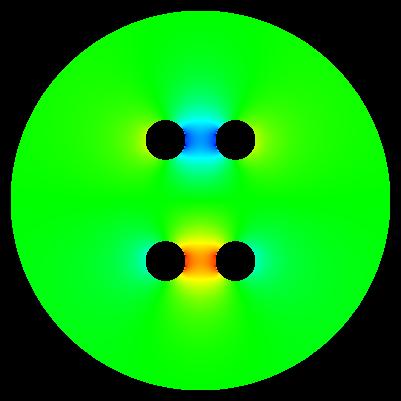
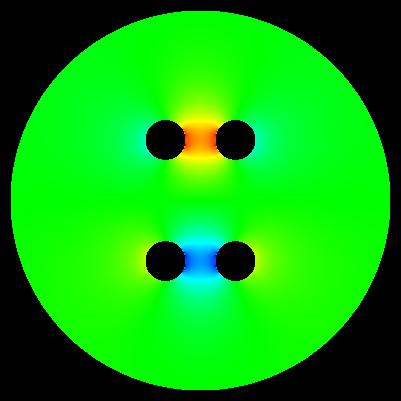
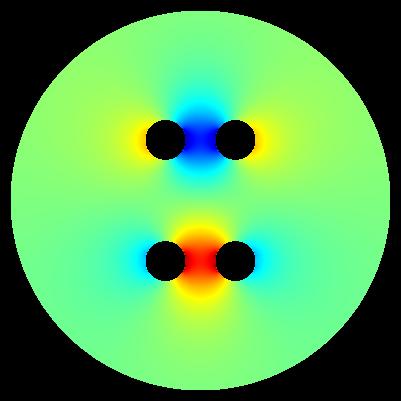
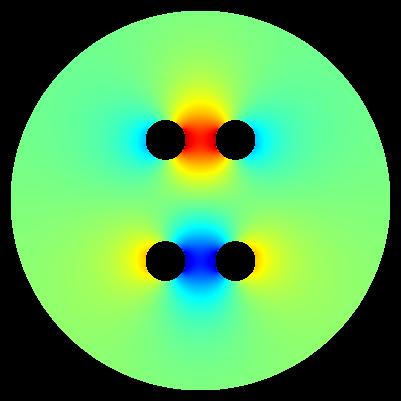
Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.


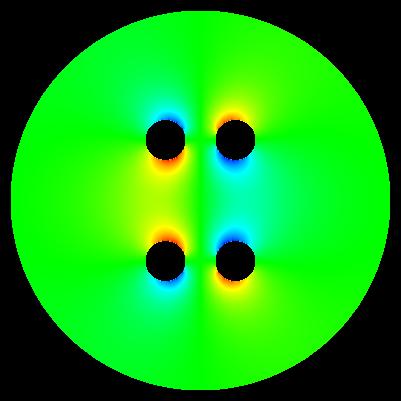
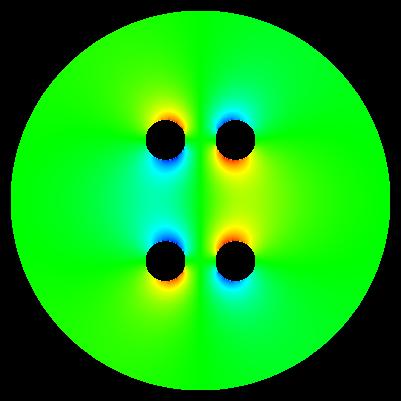
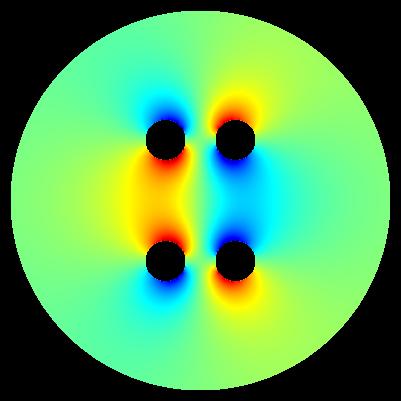
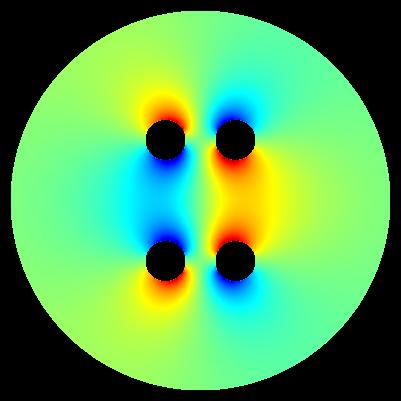
algorihm of computation: E = sqrt(E_x*E_x + E_y*E_y)
Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.



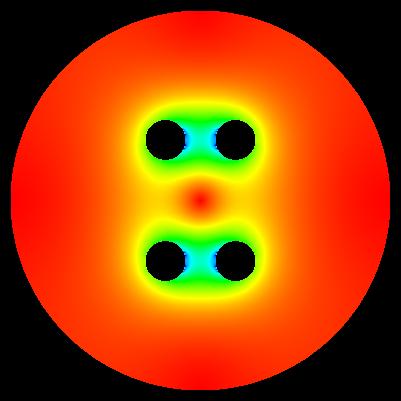

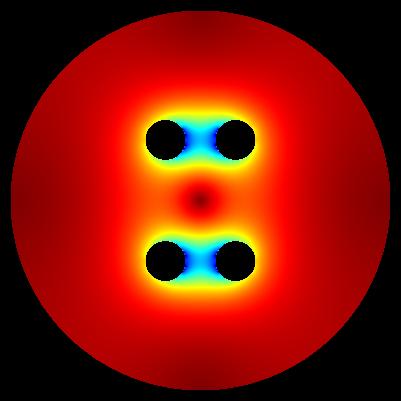
algorithm of computation: E*E = E_x*E_x + E_y*E_y
Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.



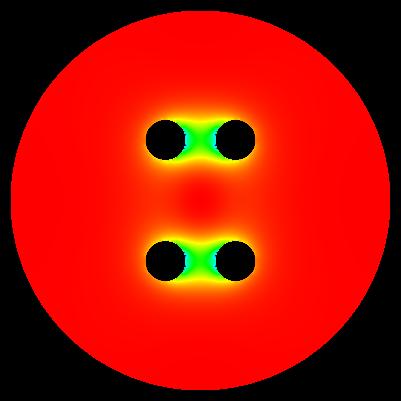

This static site does not use any cookies or gather any data.