
Windows: DEMO_XY.exe 19 Linux: ./DEMO_XY.run 19
Problem drafted in books about electron optics (multiple symmetry lenses).
Each pixel represents one mesh point.
colour white - vacuum colour red - casing 1 (U = +0.0 [V]) colour green - electrodes 2 (U = +1.0 [V]) colour blue - electrodes 3 (U = -1.0 [V])

mesh size: number of rows == 401 number of columns == 401 x == -200.0 ... +200.0 [mm] y == -200.0 ... +200.0 [mm] number of iterations >>> SUCCESS - solution V(x,y) has been found after 15111 iterations pi constant M_PI == +3.14... electrode type 1 (casing, red) boundary == +1 voltage == +0.0 [V] x_center == +0.0 [mm] y_center == +0.0 [mm] radius >= +190.0 [mm] electrodes type 2 (4 elements, green) boundary == +2 voltage == +1.0 [V] radius <= +20.0 [mm] N == +8 /* octupole */ alpha_zero == +0.0 [rad] R == +50.0 [mm] coordinates of centres of electrodes type 2: 1/4 n = +0 x_1 = R * cos(alpha_zero + 2 * n * M_PI / N); y_1 = R * sin(alpha_zero + 2 * n * M_PI / N); 2/4 n = +2 x_3 = R * cos(alpha_zero + 2 * n * M_PI / N); y_3 = R * sin(alpha_zero + 2 * n * M_PI / N); 3/4 n = +4 x_5 = R * cos(alpha_zero + 2 * n * M_PI / N); y_5 = R * sin(alpha_zero + 2 * n * M_PI / N); 4/4 n = +6 x_7 = R * cos(alpha_zero + 2 * n * M_PI / N); y_7 = R * sin(alpha_zero + 2 * n * M_PI / N); electrodes type 3 (4 elements, blue) boundary == +3 voltage == -1.0 [V] radius <= +20.0 [mm] N == +8 /* octupole */ alpha_zero == +0.0 [rad] R == +50.0 [mm] coordinates of centres of electrodes type 3: 1/4 n = +1 x_2 = R * cos(alpha_zero + 2 * n * M_PI / N); y_2 = R * sin(alpha_zero + 2 * n * M_PI / N); 2/4 n = +3 x_4 = R * cos(alpha_zero + 2 * n * M_PI / N); y_4 = R * sin(alpha_zero + 2 * n * M_PI / N); 3/4 n = +5 x_6 = R * cos(alpha_zero + 2 * n * M_PI / N); y_6 = R * sin(alpha_zero + 2 * n * M_PI / N); 4/4 n = +7 x_8 = R * cos(alpha_zero + 2 * n * M_PI / N); y_8 = R * sin(alpha_zero + 2 * n * M_PI / N); computation accuracy: eps == 1.0E-9 [V]



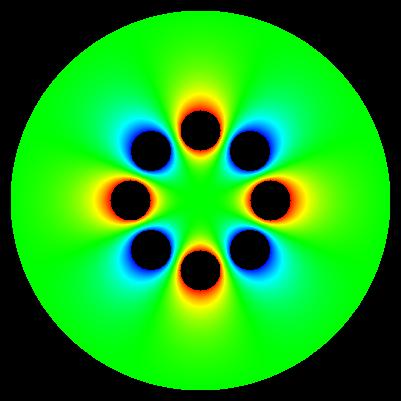
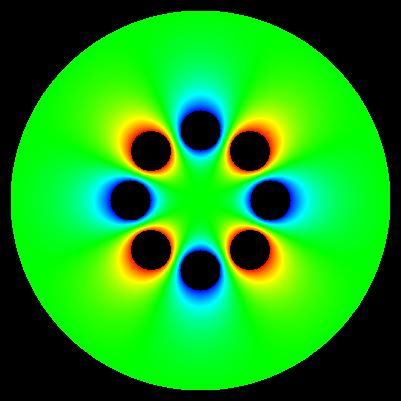
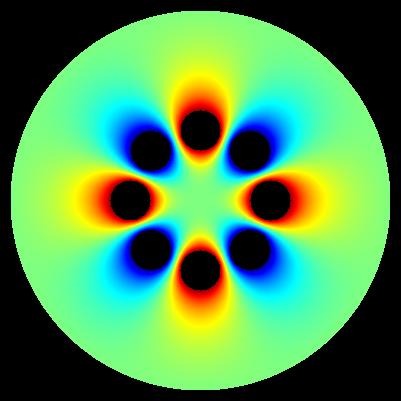
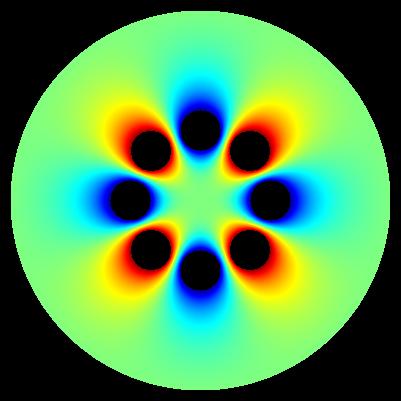
Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.






Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.






algorihm of computation: E = sqrt(E_x*E_x + E_y*E_y)
Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.






algorithm of computation: E*E = E_x*E_x + E_y*E_y
Important: determinig of exact values of E near electrode surface is generally problematic. These maps have generally illustrative character.






This static site does not use any cookies or gather any data.