Obsah preložený z anglickej verzie nástrojom Google.
Softvér Liebmann je určený na výpočty elektrónových/iónových optických systémov.
Teraz dokáže určiť rozloženie potenciálu elektrického poľa vo vákuu (kovové elektródy a vákuum, bez dielektrika).
V optike nabitých častíc je jednou z otázok určenie rozloženia elektrických a magnetických polí. Ak dobre poznáme rozloženie poľa, tak vieme napríklad určiť dráhy elektrónov v takomto poli. To sa dá využiť pri navrhovaní napríklad vedeckých alebo priemyselných zariadení.
V škole sa vo všeobecnosti učíme o elektrostatických poliach vo forme Coulombovho zákona a Gaussovho zákona. Coulombov zákon nám umožňuje určiť rozloženie elektrostatického poľa generovaného bodovými nábojmi. Existujú však problémy, ktoré presahujú túto teóriu. Ako určiť elektrostatické pole, keď majú elektródy napr. nepravidelné tvary a nemožno ich považovať za body? Vieme, že povrch kovovej elektródy má konštantný potenciál. Musíme určiť rozloženie poľa v blízkosti elektród. Niektoré elektródové systémy možno opísať pomocou pokročilých matematických metód. Našťastie, metapedagógovia vynašli aj numerické metódy, ktoré sa dajú použiť na výpočty s ľubovoľnými tvarmi elektród. Táto stránka je o takejto metóde. Elektrostatické pole je opísané Laplaceovou rovnicou. Rieši sa Liebmannovou relaxačnou metódou.
Softvér Liebmann dokáže vyriešiť Laplaceovu rovnicu.

Toto je parciálna diferenciálna rovnica, ktorá popisuje elektrostatické pole vo vákuu. Predpokladáme, že kovové elektródy majú pevné elektrostatické potenciály a sú obklopené elektrostatickým poľom. Chceme určiť rozloženie elektrostatického potenciálu tohto poľa. Chceme určiť elektrostatický potenciál vo všetkých bodoch siete, ktoré predstavujú vákuum.
Laplaceova rovnica v jednorozmernom tvare má tvar:
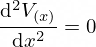
Po integrácii vedľa seba získame riešenie - jednorozmerné, rovnomerné elektrostatické pole.
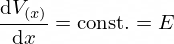
Po ďalšom integrovaní dostaneme riešenie potenciálu V(x) - lineárna funkcia.
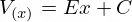
Laplaceova rovnica v 2D súradniciach X-Y (rovinná) má tvar:
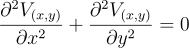
Laplaceova rovnica v 3D súradniciach X-Y-Z má tvar:
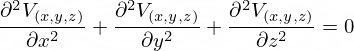
Laplaceova rovnica v 2D súradniciach Z-R (cylindrická symetria) má tvar:
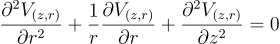
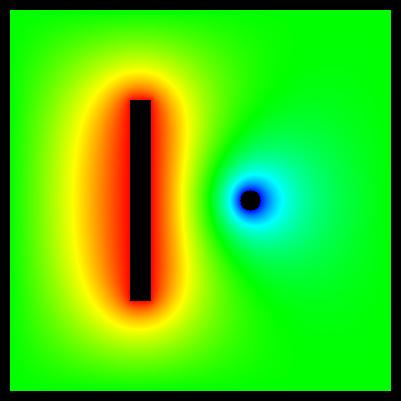
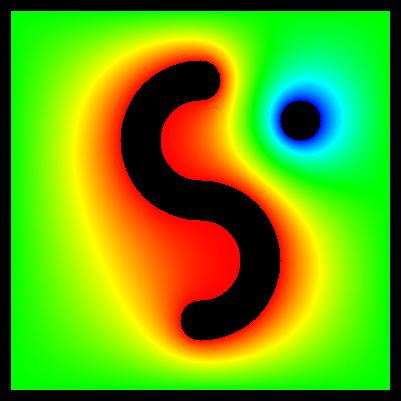
Príklad nižšie popisuje takýto neštandardný problém. Toto je dvojrozmerný problém (X-Y). Ľavý obrázok popisuje numerickú sieť, ktorá sa používa pri výpočtoch. Existujú dve rovinné dosky. Majú však nerovnakú dĺžku. Numerická sieť má 200 riadkov a 200 stĺpcov. Zelená elektróda má potenciál -1,0 [V]. Červená elektróda má potenciál +1,0 [V]. Biele body v okolí elektródy predstavujú vákuum. Chceme určiť rozloženie elektrostatického potenciálu v bodoch vákua. Dá sa vypočítať napríklad pomocou relaxačnej metódy, ktorú je možné vykonať pomocou Liebmannovho programu. Stredný obrázok popisuje výsledok výpočtu - mapovanie vypočítaného potenciálu na farby. Mapovací algoritmus je "jet" (popísaný v dokumentácii). Pravý obrázok ukazuje ekvipotenciálne čiary. Podrobný popis, ak bol tento problém zobrazený v galérii (problém č. 9).
Obrázky na tejto stránke majú rámy široké 2 pixely.



Liebmann program využíva relaxačnú metódu (konzekutívne aproximácie). Táto metóda sa nazýva aj Liebmannova relaxačná metóda. Cieľom je určenie rozloženia elektrostatického potenciálu v bodoch, ktoré predstavujú vákuum. Relaxačná metóda spočíva v spracovaní relaxačnej procedúry pre každý bod, ktorý predstavuje vákuum. Ak je tento bod vo vnútri siete, tento postup sa môže zdať jednoduchý (v 2D X-Y geometrii) (sčítanie potenciálov 4 najbližších susedov danej siete - zľava, sprava, hore, dole a potom tento súčet vynásobte 4). Po každej relaxačnej procedúre skontrolujeme, nakoľko sa nová hodnota líši od starej hodnoty uloženej v našom bode. Umožňuje nám kontrolovať maximálnu zmenu potenciálu na celej sieťke počas relaxačnej procedúry. Ak iná relaxačná procedúra spracovaná na sieti výrazne nezmení potenciálne rozdelenie, potom sa výpočet zastaví a naše potenciálne rozloženie na sieti sa považuje za novo nájdené riešenie. Získané výsledky sa zapisujú do výstupných súborov.
Softvér Liebmann je založený na robustných nástrojoch FLOSS (jazyk ANSI C, kompilátor gcc).
Liebmann je vyvíjaný v 2 prostrediach:
Liebmann je stále vo vývoji. Ďalšie podrobnosti (návody, súbory na stiahnutie, galérie) sú k dispozícii v anglickej a poľskej verzii. Bohužiaľ neviem po slovensky, takže udržiavať slovenskú verziu je príliš náročné.
Bavte sa!